js各类排序算法实现

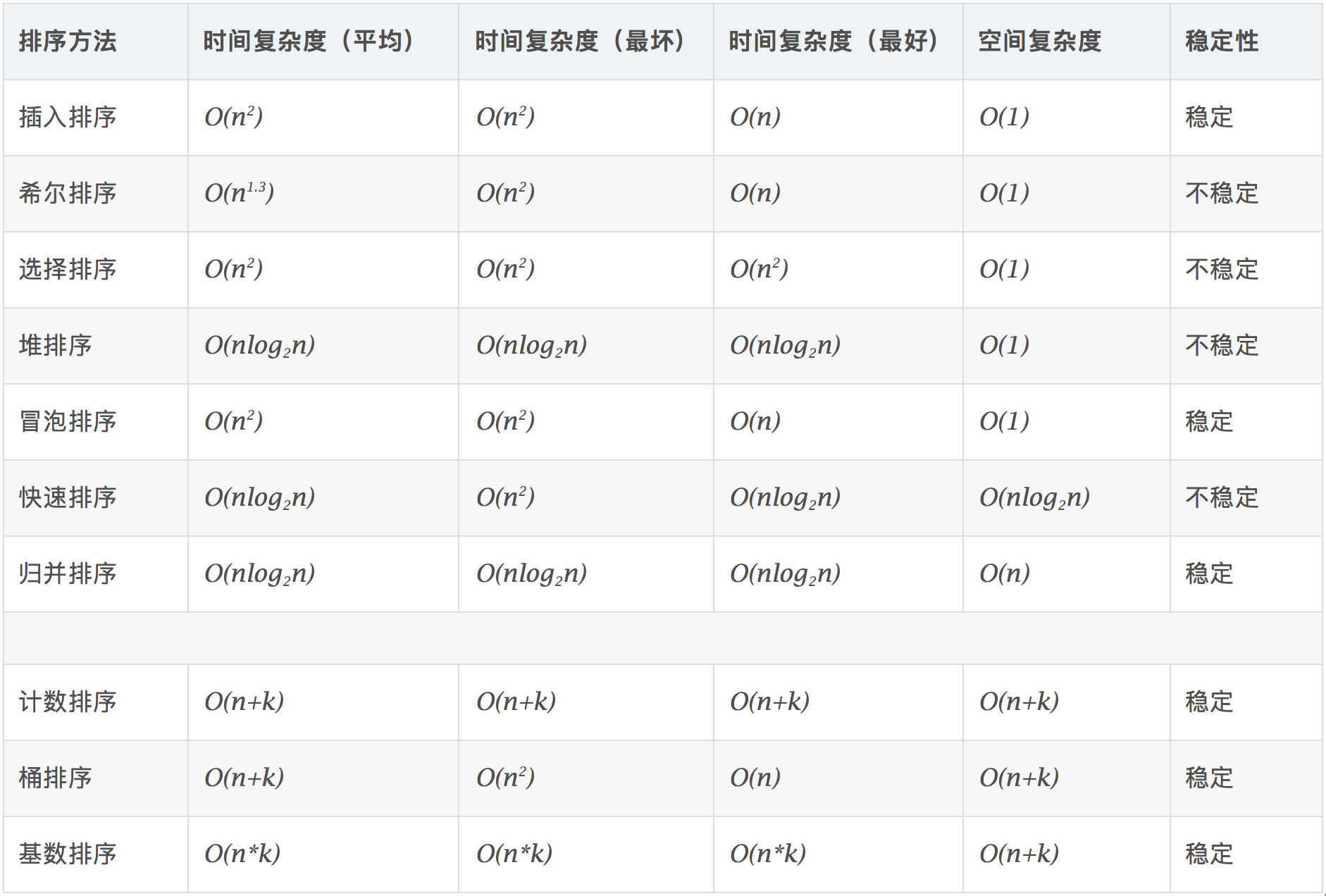
常见排序算法可以分为两大类：

非线性时间比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此称为非线性时间比较类排序。
线性时间非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此称为线性时间非比较类排序。

比较各中排序算法

在写排序算法之前，先写个交换数组中两个元素位置的方法：

function swap(arr,i,j){
    [arr[i],arr[j]]=[arr[j],arr[i]];
    return arr;
}

这是利用了es6的解构。另外，插播另一个交换两个元素值的巧妙方法： a = [b,b=a][0];

冒泡排序（Bubble Sort）

原理：

比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

javascript实现：

function BubbleSort(arr){
    if( !arr || !arr instanceof Array || arr.length <= 0 ){
        return; 
    }
    let len = arr.length;
    for( let i = 0 ; i< len; ; i++){
        for (let j = 0;j< len - i - 1 ; j++ ){
            if( arr[j + 1] < arr[j] ){
                swap(arr,i,j);
            }
            
        }
    }
    return arr;
}

console.log( BubbleSort([3,992,135,234,231]) );

选择排序(Selection-sort)

选择排序是一种简单直观的排序算法。

它的工作原理：

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置；
然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
以此类推，直到所有元素均排序完毕。

javascript实现：

function selectionSort(arr){
    if( !arr || !arr instanceof Array || arr.length <= 0 ){
        return;
    }
    let len = arr.length;
    let currentMinIndex,currentMin;
    for(let i = 0 ; i < len ; i++){
        currentMin = arr[i];
        currentMinIndex = i;
        for( let j = i ; j < len ; j++){
            if( arr[j] < currentMin ){
                currentMin = arr[j];
                currentMinIndex = j;
            }
        }
        if(currentMinIndex !== i ){
            swap(arr,i,currentMinIndex);
        }
        
    }

    return arr;
}

console.log( selectionSort([999,231,324,552,35,1]) );

插入排序（Insertion Sort）

插入排序的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入：

从第一个元素开始，该元素可以认为已经被排序；
取出下一个元素，在已经排序的元素序列中从后向前扫描；
如果该元素（已排序）大于新元素，将该元素移到下一位置；
重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
将新元素插入到该位置后；
重复步骤2~5。

javascript实现：

function insertionSort(arr){
    if( !arr || !arr instanceof Array || arr.length <= 0 ){
        return;
    }
    let len = arr.length;
    for(let i = 1 ; i < len; i++){
        let currentIndex = i;
        let currentValue = arr[i];
        while( currentIndex >= 1 && currentValue < arr[currentIndex-1] ){
            arr[currentIndex] = arr[currentIndex-1];
            currentIndex--;
        }
        arr[currentIndex] = currentValue;
    }
    return arr;

}
console.log(insertionSort([999,123,21,3,56,778]));s

希尔排序（Shell Sort）

1959年Shell发明，第一个突破O(n2)的排序算法，是简单插入排序的改进版。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述：

选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
按增量序列个数k，对序列进行k 趟排序；
每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

归并排序（Merge Sort）

归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

把长度为n的输入序列分成两个长度为n/2的子序列；
对这两个子序列分别采用归并排序；
将两个排序好的子序列合并成一个最终的排序序列。

快速排序（Quick Sort）

快速排序有两种

function quickSort(arr){
  if(!arr || !arr.length){
    return [];
  }
  
  let start = arr[0];
  
  let left = []; 
  let right = [];
  
  for(let i = 1 ; i< arr.length ; i++){
    if(arr[i]< start){
      left.push(arr[i])
    }else{
      right.push(arr[i])
    }
  }
  return quickSort(left).concat([start]).concat(quickSort(right));
}

let output = quickSort([11,235,13,123,10,2,13,231,3,2,1,23]);

console.log(output)